Advent of Code 2020 Day 12

As the Iowa game started at 8 pm on Friday, and I knew that I was already going to be up until about 10 pm, and I still had laundry in the dryer, which because I'm somewhat lazy, I tend to leave down there for way too long, so I figured I would stay up until 11 pm to complete day 12 when it was released.

The Day 12 puzzle part one set up to move a ship based on a specified set of movements (the puzzle input file) where you are either moving a specified distance north, east, south, west, or "forward" OR you are rotating to the left (counter-clockwise) or to the right (clockwise) by 90, 180, or 270 degrees. This is really just tracking the movement of the ship. The final answer for part one was the Manhattan Distance of the current location of the ship at the end of movement to the original location. When you start at an origin point, this is effectively the sum of the absolute values of the x and y direction.

I will admit, I did part two in a very strange way, that should've been done better, but I guess that's my lack of sight (and desire to track everything or something like that). But for part two the change is that rather than your ship, there is both your ship and a waypoint. The north, south, east, west movements are ONLY movements for the waypoint (which starts 10 spaces east and 1 space north of your ship). Rotation (Left and Right) is rotation of the waypoint around the ship itself. Because I was feeling like I needed a visual, I drew out the base example (based on the starting position of the waypoint) with my ship being at (0, 0) and the waypoint "start" being at (10, 1) indicating 10 east, 1 north.

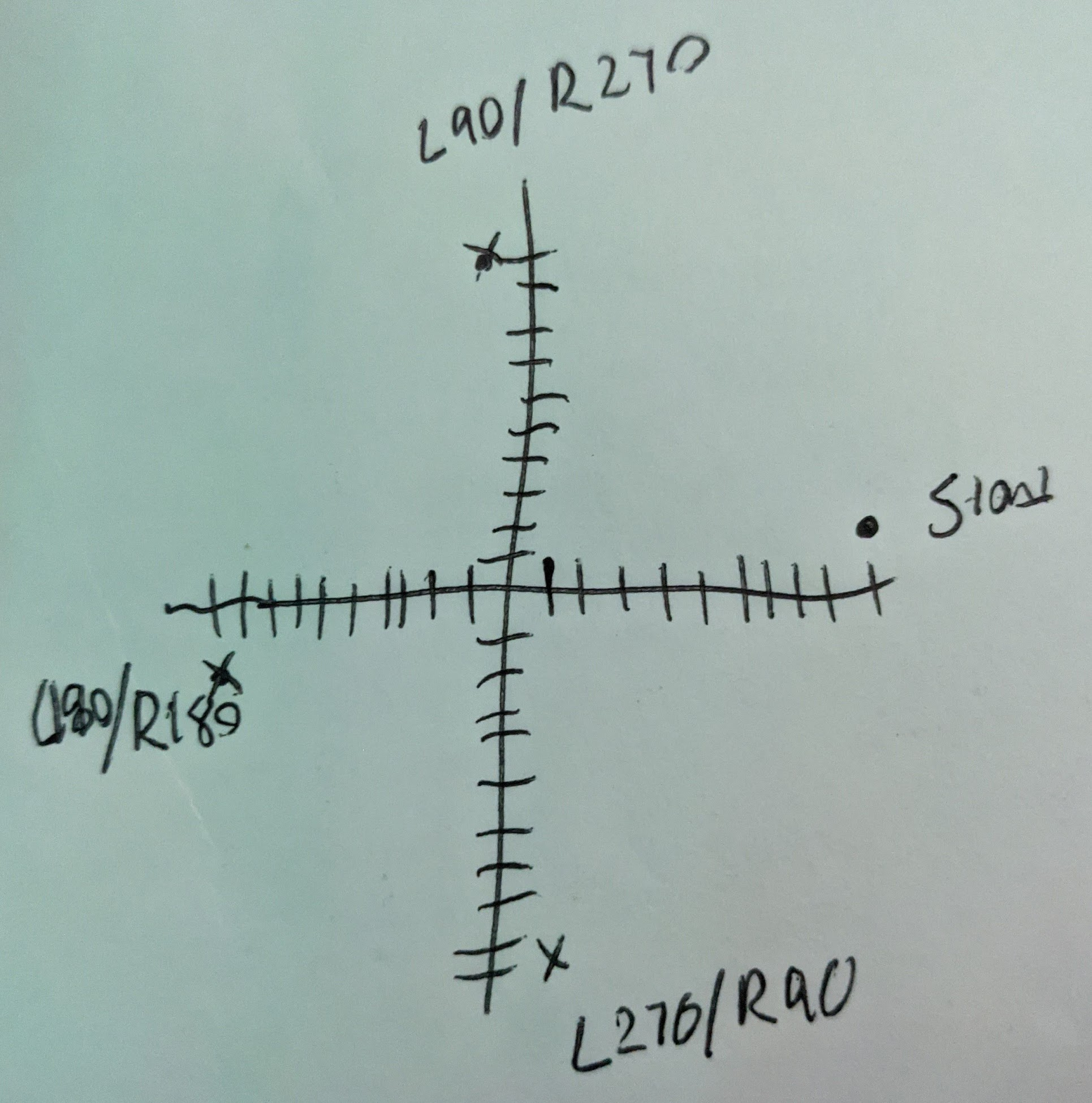
So, as you can see, rotating left is the same as rotating right by 360-value so we could simplify logic there. And all that's happening is the dX and dY from the ship are flipping, when rotating left 90/right 270, your new x is x-dY, your new y is y+dX.  When rotating left 180/right 180, your new x is x-dX, your new y is y-dY. When rotating left 270/right90, your new x is x+dY, your new y is y-dX. The ship itself only moves when the forward direction is called, and when the ship moves, the ship moves in the direction of the waypoint, but the waypoint continues to be the same distance from the ship even while the ship moves, so in the example provided in the problem, if the ship moves forward 10 times (now the distance means how many times the ship moves to the point that the waypoint is at) and the waypoint starts at 10 east, 1 north your ship would move to 100 east, 10 north and the waypoint would then be located at 110 east, 11 north to maintain that 10 east, 1 north offset. If after the forward movement, the waypoint receives the direction to rotate left 90 degrees, the new position of the waypoint would be 99 east, 20 north, because we're subtracting 1 from the east, and adding 10 to the north from the ship.

In my solution, I did actually track BOTH the ship movement and the waypoint location. It is 100% possible to do this only tracking the relative location of the waypoint from the origin, and when moving forward, simply adding the appropriate distance moved to a variable that assumes (0, 0) is the only "location" of the ship, this means the logic to rotate the waypoint about the ship is less about calculating differences and more about just manipulating the x and y coordinates of the waypoint. This was the fastest that I was able to complete the challenge with respect to comparison to other people, which was a bit of an accomplishment for me.

If you want to join my Advent of Code leaderboard, feel free to join with the code: 699615-aae0e8af.